Merasionalkan penyebut bentuk akar pangkat dua sudah sering kita jumpai, namun merasionalkan bentuk akar pangkat tiga barangkali jarang kita jumpai, karena tidak semua buku matematika SMA membahas tentang ini.
Pertama yang perlu kita perhatikan definisi dari sekawan. Selama ini di buku-buku dijelaskan bahwa sekawan dari (a - b) adalah (a + b), dan sebaliknya. Definisi ini perlu kita kembangkan sebagai berikut: Dua bentuk akar dikatakan sekawan bila kedua bentuk akar itu dikalikan menjadi bilangan rasional.
Misal:
-
dan
adalah sekawan, karena bila kedua bentuk akar ini dikalikan hasilnya
(Rasional).
dan
adalah sekawan, karena bila kedua bentuk akar ini bila dikalikan hasilnya 2 (ingat rumus (a - b)(a + b)).
dan
adalah sekawan, karena hasil kalinya adalah 3. Gunakan rumus
. Untuk contoh 3 perlu dijelaskan:
= ( )(
)(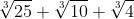 )
)
= ( )(
)(^{2}%20+%20\sqrt[3]{5}\sqrt[3]{2}%20+%20(\sqrt[3]{})^{2}) )
)
= ^{3}%20-%20(\sqrt[3]{2})^{3})
= 5 - 2
= 3
Konsep ini nanti kita gunakan untuk merasionalkan penyebut bentuk akar pangkat tiga
Contoh Soal:
Rasionalkan bentuk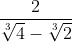 !
!
Penyelesaian:
}{2}=\sqrt[3]{16}+\sqrt[3]{8}+\sqrt[3]{4})

gak jelas tau gak,gak mutu
BalasHapusYang bagus sperti apa?
Hapusjelas kok, mungkin orang yang baca ndak tau maksudnya
HapusIni jelas banget lho. Dan bisa di aplikasikan ke berbagai macam soal.
HapusYang komen kayak hater di atas, brarti gk ada otaknya. Emang, untuk jenis soal kayak gini terbilang langka, jadi emang susah cari contoh. Tapi, sudah mau berbagi hal berguna begini, layak dpet double like, deh. Mohon dihargai ya
kurang rapi mas
BalasHapusBagus kok ada ilmunya, baru tau ada macam2 sekawan, yang ku tau yang nomor dua aja selama ini
BalasHapusYang paling atas hater tuh, pak. Gak usah d tanggepin
BalasHapustapi jujur ini mantep lo
BalasHapusjarang-jarang ada yang begini
Bermanfaat pak... Mantap..
BalasHapusUntuk pangkat 4 dan lainnya jg bsa dtentukan dgn bntuan horner..coba deh sobat. Indahnya berbagi.
BalasHapusOoh..begituu...
BalasHapusSkrg sya paham. Sangat membantu saat bertemu soal2 limit tak hingga bentuk akar.
Terima kasih...
salut untuk bapak...dapat ilmu baru saya
BalasHapusGood Joooob 😄😄😄😄😄
BalasHapusTerimakasih yg sudah membuat artikel ini.. Sangat bermanfaat sekali, saya jadi paham nih.. 😁😁Hehe
BalasHapusTeruskan ya (y)
Terimakasih yg sudah membuat artikel ini.. Sangat bermanfaat sekali, saya jadi paham nih.. 😁😁Hehe
BalasHapusTeruskan ya (y)
Akhirnya saya tau akar sekawan dari akar 3. Nyari materi ini akhirnya ada yg bahas juga. Ntappps
BalasHapusBagus ilmunya,smoga bermanfaat untuk kita smua
BalasHapusTerima kasih, sangat membantu sekali
BalasHapusTerima kasih banyak ilmunya. Sangat membantu.
BalasHapus